Quanto fa 6:2(1+2)?
L’altro giorno, mentre ero sul divano a riposarmi, una mia amica mi ha girato questa semplice domanda: quanto fa 6:2(1+2)?
Cerchiamo di risolverlo nella maniera più “scientifica” possibile visto che esistono opinioni discordanti riguardo il risultato.
La prima cosa che insegnano a matematica è l’ordine delle operazioni, tale logica può essere riassunta così (PEMDAS):
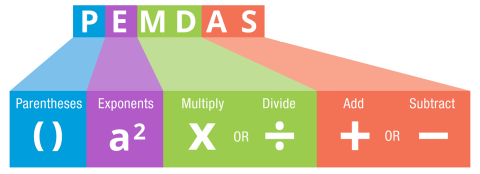
Ossia:
- Parentesi
- Potenze
- Moltiplicazioni e divisioni (da sinistra a destra)
- Addizioni e sottrazioni (da sinistra a destra)
Cerchiamo di applicare tali regole alla risoluzione dell’espressione in oggetto:
- Eseguiamo le operazioni raggruppate tra parentesi:
6:2(3) - Eseguiamo le moltiplicazioni/divisioni:
3(3)che diventa poi9
Il risultato è pertanto 9, sia Google che Wolfram ci danno ragione.
Da notare come esiste anche un operatore nascosto, la moltiplicazione, quindi in realtà l’espressione originaria dovrebbe essere scritta 6:2x(1+2).
Perchè c’è gente che si ostina a dire che il risultato di tale espressione è 1?
Semplicemente per il fatto che sono portati a pensare l’espressione come una frazione, ossia 6:[2(1+2)].
Come potete vedere questa assunzione di fatto porta ad allontanarsi dall’espressione originale in quanto si aggiungono delle parentesi che cambiano l’ordine delle operazioni.
Problem solved!
Ehm. Non so cosa dicono Google e worfram, ne la matemetica, ma secondo PEMDAS che citi, sei tu a fare l’operazione errata. Dice prima le moltiplicazioni. Poi le divisioni. Quindi le quadre che metti nell’esempio sotto sono giuste.
Una operazione scritta in questo modo cmq genera ambiguità.
Se sostituisco le (2+1) con x ed uso il segno di frazione, viene 6/2x che mi risolvi come 1 senza pensarci.
Se la interpreti invece come 6/2 * (2+1) invece (scritta su carta ė più chiara) hai ragione tu.
Non so quale sia la cosa più giusta essendo ignorante, ma tenendo PEMDAS come specifica il risultato giusto ė 1.
Ciao Yuri,
grazie del commento, per la precisione PEMDAS sta per:
1. Parentesi
2. Potenze
3. Moltiplicazioni e divisioni (da sinistra a destra)
4. Addizioni e sottrazioni (da sinistra a destra)
Ad esempio 15:3×4 non è come scrivere 15:12 bensì 5×4.
Riguardo al tuo ultimo esempio:
In quel caso giustissimo ma nell’esercizio precedente no poichè la parentesi non la risolvi, bensì la sostituisci con un segno di moltiplicazione, infatti 6÷2(3) devi prima di tutto risolverla, ma per farlo sei anche costretto a risolvere l’operazione, quindi il risultato è 1
Da che mi ricordo io si fanno prima le moltiplicazioni, le divisioni e poi somma e sottrazione, l’espressione io l’ho interpretata come frazione ma ciò non toglie che l’ordine delle operazioni da svolgere sia quello sopra indicato, per me il risultato è 1
Leggi attentamente il post, ci sono delle regole ben precise, vanno seguite…e se le segui correttamente vedrai che il risultato è 9.
Ma non capisco cosa ci sia di così tanto difficile. La precedenza alla parentesi, SOLO A CIÒ CHE È DENTRO LA PARANTESI, non dovete moltiplicare la parentesi per 2. Dopo le parentesi si fanno le moltiplicazioni E le divisione ( non vuoldire prima le moltiplicazioni e poi le divisioni). Quindi è una cosa banalissima. 6÷2×3=9. Se volete usare la frazione 6/2 × 3=3×3=9.
vero, 15:3X4 non è 15:12 è giustamente 5×4
MA
15:3(2+2) ( come nel famoso esempio…..HA LA PARENTESI) e quindi è 15X12…
Svolgi prima ciò che c’è scritto dentro la parentesi quindi 15:3X(2+2) diventa 15:3X4, ossia 5X4 che fa 20
Infatti hai scritto 2 operazioni diverse, poiché:
15÷3(2+2)=15/12
15÷3×(2+2)=20
Questo poichè se non viene espresso il segno (×) affianco alla parentesi di conseguenza viene considerato come un numero associato alla parentesi ma se è presente, tanto di cappello allora solo e solamente in quel caso abbiamo 9 altrimenti fa 1
In entrambi gli esempi nn capisco perchè risolvete prima la divisone (15:3 oppure 6:2) mentre il metodo pemdas dice chiaramente di risolvere prima la moltiplicazione
Ciao,
ho aggiornato l’immagine che riassume il PEMDAS in modo che ne capisca il funzionamento anche chi non legge attentamente tutto il post.
Perché si risolvono da sinistra verso destra
PeR convezione
Il metodo ti dice che si risolvono da sinistra verso destra, ovvero nell’ordine in cui le trovi in assenza di parentesi. Ma com’è possibile che non vi sia chiaro?
La tua risposta sarebbe corretta se non fosse per il fatto che in matematica le espressioni e tutto quello che ne deriva si svolgono prendendo delle priorità, ovvero, in questo caso, le parentesi
quanto è brutta l’ignoranza………………….metodi………………………quello dice………………….., la matematica è fatta di regole ben precise che nn lasciano spazio alle interpretazioni……………….quindi invece di dire bagianate andate a vedere le regole …….che dicono: prima parentesi poi potenze poi moltplic e divisioni e in ultimo addizioni e sottrazioni punto finiti i discorsi queste sono regole nn punti di vista mie cari filosofi della matematica !!!!!!!!!!!!
Talmente brutta che tu sei il primo ad esserlo
Almeno esiste uno concreto
Chi sarebbero i filosofi della matematica Alessandro? Prima le moltiplicazioni e le divisioni DA SINISTRA VERSO DESTRA, ovvero:
2×6:3=4 (si svolge prima la moltiplicazione)
4:2×3=6 (si svolge prima la divisione
Ergo:
6:2(2+1)= 6:2×3= 9
Dove sono le opinioni? Queste sono regole.
Scusate ma non vanno eliminate per prima le parentesi??
Perciò 6 :2 x (3) = risolvi prima la parentesi xké ha la priorità (2 x 3 fa 6 e quindi) quindi 6 : 6 = 1
Va svolto per prima ciò che c’è dentro le parentesi, ma questo non vuol dire che ciò che è fuori e vicino alla parentesi vada svolto anch’esso per primo.
6:2×3 è 3×3 ossia 9.
Facendo il calcolo con una calcolatrice scientifica il risultato è 1
6:2(2+1)
Va fatta prima la parentesi, giusto?
2+1=3
Come scriviamo i resto delle operazioni?
6:2×3
Quale è la prossima operazione?
La moltiplicazione, giusto?
2×3=6
Cosa ci rimane?
6:6=1
Fine
E’ un film con un finale errato, mi spiace.
6:2×3, va svolta prima la divisione e poi la moltiplicazione, da sinistra a destra. Quindi il risultato è 9.
Per primo (…) poi “X” e “:” in ordine da sinistra alla destra… 6:2×3=9 .. poi se c’è “+” e “-” sempre in ordine dalla sinistra alla destra
E’ difettosa o l’hai usata male ;-)
Bhe, date la definizione giusta e poi date il risultato sbagliato. Va bene vogliamo contare questo famoso pemdas? Va bene allora preso 6:2(1+2) ho che:
1) parentesi: 6:2(1+2) diventa 6:2(3);
2) potenze: 6:2(3) diventa 6^(-1)x2(3);
3) moltiplicazione o divisione: 6^(-1)x2(3) diventa 6^(-1)x6 cioè 6/6=1.
Ragazzi per favore non dite stronzate su internet, che po’ ci sono ragazzini di 10 che le leggono e mettono in dubbio che sia un ingegnere (assurdo)
Non scomoderai le potenze (oltretutto inserite cambiando l’espressione), 6/2*3 va eseguito da sinistra verso destra in quanto sono tutte operazioni (divisione e moltiplicazione) con la stessa priorità. Concordo invece con il tuo ultimo paragrafo.
Senza convenzioni (come se un programmatore non dettasse variabili) come fate a dire che sia corretto 9 o corretto 1?
Nel questionario dove sta la convenzione che in matematica SEMPRE va indicata prima di porre un quesito?
E non fatemi maestri, purtroppo questi quesiti nascono per farvi accanire gli uni contro gli altri.
Leggete qui se conoscete l’inglese e fate pace
http://www.slate.com/articles/health_and_science/science/2013/03/facebook_math_problem_why_pemdas_doesn_t_always_give_a_clear_answer.single.html
Veramente da quanto ricordo io, proprio perché scritta in questo modo, il risultato è 1:
6/2(1+2)=6/2(3)=6/6=1
Viceversa, se si fosse scritto
( 6÷2 ) ( 1+2 )= il risultato sarebbe 9
6÷2=3
1+2=3
(3) (3)=9
6/2(3) fa 9 in quanto le operazioni devi svolgerle da sinistra verso destra, il fatto che ci sia la parentesi indica solo che devi dare priorità alle operazioni al suo interno.
Il problema e’ Che quando fai la somma togli la parentesi mentre anche se fai la somma la parentesi rimane …….quindi fa 1
Una volta svolta le operazioni dentro la parentesi, può essere tolta senza problemi.
Il motivo della discussione sta nel modo in cui è scritta l’operazione… che è ambigua, in quanto interpretabile in diversi modi.
Ho visto un’immagine in cui veniva spiegato il PEMDAS che recitava:
6(5+3) = 6*8= 48 (right!)
6(5+3) = 30+ 3= 33 (wrong!)…. e certo che è sbagliato, perché il corretto svolgimento è 30+18= 48, proprio in virtù delle parentesi.
Detto questo dipende se uno interpreta la moltiplicazione scritta in quel modo davanti alla parentesi come parte integrante di essa o meno.
Mi spiego meglio:
Se interpreto 2(1+2) come una scomposizione in fattori di polinomi, posso asserire che è corretto scriverlo come (2+4) = (2*1 + 2*2) = 2(1+2) e ciò implicherebbe sempre lo stesso risultato: 6 , che tornando al quesito iniziale porterebbe al risultato finale di 1 (6:6=1)
quindi
3/3y=(3/3)(y)=y
ma tutti sappiamo che
3/3y=3/3y=1/y
Il metodo pemdas non dice prima la moltiplicazione e poi la divisione, attenzione leggete bene. Dice prima la moltiplicazione e poi la divisione nell’ordine in cui si presentano da sinistra a destra. Se c’è prima la moltiplicazione si risolve la moltiplicazione, altrimenti come in questo caso, la divisione.
Allora io ti faccio una domanda: quanto fa 6:2×3?
Il risultato è uno. L’ordine delle operazioni è molto chiaro, prima le parentesi, poi le potenze, moltiplicazioni, divisioni, addizioni, sottrazioni. Insistere che le operazioni si svolgono da destra a sinistra o da sinistra a destra è un modo di arrampicarsi sugli specchi.
Vi state sbagliando, perché l’espressione è scritta così: 6÷2(1+2)
e non così: 6÷2x(1+2)
Quindi è più corretto risolvere prima la parte “2(1+2)” come se fosse tutto un blocco e poi fare la divisione. Quindi il risultato finale corretto è 1